Na początku warto wyjaśnić, co oznaczają tajemnicze granice ciągów. Granica ciągu to pojęcie, które informuje nas o tym, do jakiej wartości zbliżają się wyrazy ciągu, gdy podejmujemy próbę zbliżenia się do nieskończoności. Można to zobrazować poprzez porównanie do podchodzenia do krawędzi przepaści – im bliżej jesteśmy, tym lepiej dostrzegamy, co znajduje się na dnie. Niestety, w przypadku niektórych ciągów, możemy trafić w przepaść bez dna zamiast wartości! Takie przypadki są również istotne, ponieważ oznaczamy wtedy, że ciąg „dąży do nieskończoności”.
Aby obliczać granice ciągów, matematycy opracowali tablicę wzorów, która może przypominać coś w rodzaju menu w restauracji – wystarczy tylko wybrać odpowiednią pozycję! Wśród kluczowych wzorów znajdują się różne ciągi, takie jak \(\frac{1}{n}\) (gdzie granica to oczywiście 0). Dla ciągu geometrycznego z malejącą rządową wartością, na przykład w przypadkach, gdy \(q<1\), także uzyskuje się 0. Przy tym, jeżeli zaczynasz eksperymentować z potęgami \(n\), pamiętaj, że \(n^k\) zawsze dąży do nieskończoności, gdy \(k\) jest dodatnie – więc poprowadzi cię prosto do nieba, zamiast w stronę ziemi!

Nie daj się zwieść złożonym działaniom arytmetycznym, które możesz zastosować do granic ciągów. Mówiąc obrazowo, jeśli potrafisz dodawać, odejmować, mnożyć lub dzielić dwa ciągi \(a_n\) i \(b_n\), to granice tych operacji pozostają niezwykle przewidywalne. Pomnażając granice, sumując je lub obliczając iloraz (o ile nie dzielisz przez 0), wszystko przebiega zgodnie ze zdrowym rozsądkiem. Matematyka uwielbia porządek – jednak w sytuacji, gdy jeden z ciągów mieszają wszystkie wartości z nieskończonością, wtedy musisz się bardziej napocić, aby dotrzeć do twardej prawdy!
Reasumując, granice ciągów stanowią kluczowe elementy, które przy odrobinie praktyki łatwo zgarniesz jak cukierki z festynowej torby. Im więcej przykładów obliczysz, tym bardziej zauważysz, że matematyka staje się przyjemnością, a nie męką. Nie zapominaj również o nowoczesnych narzędziach online, które szybko wyczarują wyniki – a zanim się obejrzysz, staniesz się mistrzem granic! Więc do dzieła!
Poniżej przedstawiam kilka kluczowych wzorów dotyczących granic ciągów:
- \(\frac{1}{n}\) – granica 0
- ciąg geometryczny z \(q<1\) – granica 0
- \(n^k\) – dąży do nieskończoności dla dodatniego \(k\)
Praktyczne zastosowanie kalkulatora: Jak poprawnie wprowadzać dane?

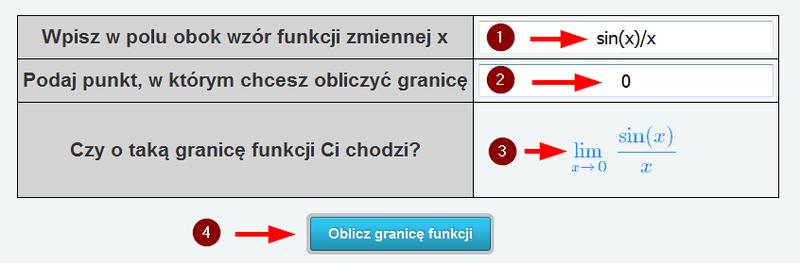
Serdecznie zapraszam do fascynującego świata kalkulatorów, które przypominają magiczne różdżki w rękach tych, którzy pragną uprościć swoje matematyczne zmagania. Kiedy już zdecydujemy się na wykorzystanie tego cudownego narzędzia, musimy wiedzieć, jak prawidłowo wprowadzać dane. W końcu nikt nie chce, aby zamiast „końca” otrzymać „początek” obliczeń! Takie sytuacje mogą zdarzyć się, gdy nie dostarczymy kalkulatorowi odpowiednich informacji!
Aby rozpocząć, upewnijmy się, że mamy wszystkie niezbędne dane przed naciśnięciem „enter”. Przemyślmy, co dokładnie chcemy policzyć: granicę ciągu, czy raczej limit funkcji? Dobrze jest mieć wszystko pod kontrolą, ponieważ w przeciwnym razie nasz kalkulator przypominać będzie dziecko zgubione w supermarkecie. Wszyscy zaczynają się gubić! Dlatego wypełnijmy pola prawidłowymi wartościami i wybierzmy odpowiednią opcję obliczeń bez zbędnych emocji.

Tymczasem warto wykonać mały test na cierpliwość! Sprawdzanie, czy wprowadzone przez nas wartości są prawidłowe, to dobry zwyczaj. Nic bardziej frustrującego nie istnieje niż błąd przy wprowadzaniu wartości, który rzutuje na nasze wyniki matematyczne. Uwaga, to jak taniec – możliwe jest, że wszystkie dowcipy umkną, a my zostaniemy z niezrozumiałymi cyframi na ekranie. Zatem sprawdź swoje dane dwa razy, ponieważ po kliknięciu „oblicz” nie można już wrócić!
Pamiętajmy, że dobrze wpisane dane stanowią klucz do sukcesu! Oto kilka kroków, które warto podjąć, aby upewnić się, że nasze dane są poprawne:
- Zrozumienie problemu i celów obliczeń.
- Dokładne wprowadzenie wartości do kalkulatora.
- Podwójne sprawdzenie wprowadzonych danych.
- Wybranie odpowiedniej funkcji obliczeń.

Kalkulatory, mimo iż są niezwykłymi narzędziami, jak każde tworzenie w świecie, mają swoje ograniczenia. Z tego względu warto być aktywnym – nawet z kalkulatorem w ręku, nie zaszkodzi odrobina intelektu! Jeśli poświęcimy chwilę na zrozumienie wzorów i funkcji, które się ze sobą łączą, nasza współpraca z kalkulatorem będzie równie satysfakcjonująca, co sukces przy rozwiązywaniu najbardziej skomplikowanych równań!
Analiza wyników: Interpretacja otrzymanych granic ciągu
Analiza wyników granic ciągu otwiera niezwykły świat matematyki, w którym liczby tańczą w rytm zbieżności i rozbieżności. Dzięki odpowiednim właściwościom możemy zaobserwować, jak zmienia się zachowanie równania wraz ze wzrostem wartości zmiennej. Oczywiście, mało co w życiu okazuje się prostsze od momentu, w którym zrozumiemy, że przy obliczaniu granic ciągów, końcowe wartości mogą być naprawdę zaskakujące — zaczynając od zera, przez zbieżność do nieskończoności, aż po bardziej przystępne liczby. To starzy, dobrzy matematycy wpadli na pomysł wprowadzenia nas w błąd, kiedy sprawy zdają się być jasne.
Nie możemy zignorować tego, jak bardzo pomocne są podstawowe wzory granic ciągów. Często słyszymy, że matematyka oferuje „krótkie trasy”, które przyspieszają naszą podróż do wyników. Na przykład ciągi geometryczne regularnie zbliżają się do zerowej granicy przy odpowiednich wartościach, a te wzory, jako praktyczne narzędzia, stają się naszymi najlepszymi przyjaciółmi. W ten sposób, korzystając z paru prostych wzorów i przekształceń algebraicznych, mamy możliwość zanalizowania nie tylko konkretnego ciągu, ale także jego charakterystyki.
Podczas obliczania granic warto mieć na uwadze, że matematyka potrafi być złośliwa, a granice mogą niespodziewanie czaić się w różnych miejscach. Czasami konieczne okazuje się stosowanie różnych twierdzeń — od standardowych do bardziej zaawansowanych trików, które przypominają magię kart. Przykładem jest potężne twierdzenie o trzech ciągach, które umożliwia wyciąganie wniosków, nawet gdy sytuacja nie jest oczywista. Analiza granicy z użyciem tego narzędzia przypomina sztuczkę z chusteczką — nie ma czasu na długie rozmyślania, a wyrafinowane przybliżenia unoszą się w powietrzu!
Dlatego, jeśli przyjdzie Ci zmierzyć się z granicami ciągów, pamiętaj, że każdy krok, wzór i technika obliczeń tworzy kawałek większej układanki. Zawsze warto spojrzeć na problem z różnych perspektyw — niejednokrotnie to, co wydaje się nieosiągalne, okazuje się być zaledwie w zasięgu ręki. W matematyce, jak w życiu, kluczowym elementem jest nie zrażać się trudnościami, lecz uczyć się na podstawie naszych doświadczeń. W ten sposób, korzystając z humoru i nieco teorii, zyskujemy szansę na zrozumienie tych napiętnowanych liczb w ich szalonej podróży ku granicy.
Poniżej przedstawiam kilka kluczowych wzorów granic ciągów, które mogą być niezwykle przydatne:
- Wzór granicy dla ciągów arytmetycznych
- Wzór granicy dla ciągów geometrycznych
- Twierdzenie o trzech ciągach
- Reguła de l’Hospitala dla granic
Najczęstsze błędy przy obliczaniu granic: Jak ich unikać?
Obliczanie granic ciągów często przypomina matematyczny rollercoaster, zwłaszcza dla wielu uczniów. Nie można uwierzyć, że nawet przy najprostszych zadaniach można popełnić błędy! Wśród najczęstszych potknięć znajdują się m.in. niepoprawne uproszczenia oraz ignorowanie reguł działania na granicach. Aby uniknąć tych pułapek, przypomnijmy sobie kilka podstawowych zasad. Wśród nich znajduje się twierdzenie o działaniach arytmetycznych – jeśli znamy granice dwóch ciągów, możemy je swobodnie dodawać, odejmować, mnożyć, a nawet dzielić, o ile nie dzielimy przez zero, bo wtedy zaczynają się schody!
Niezwykle istotne jest pamiętanie, że dzielenie przez rozbieżne ciągi może prowadzić do zgubnych skutków. Gdy dany ciąg dąży do nieskończoności, jego odwrotność może w pewnym momencie skierować nas w stronę zera. Wyłączenie swojego „wrodzonego pesymizmu” oraz gotowości do negowania oczywistych faktów bywa kluczowe. Nie zgubmy się w złożonych liczbach, bo można w tym momencie wylądować jak przysłowiowy „zając na drodze”. Nagle coś nam się przypomni, a zamiast dotrzeć do celu, wpadniemy w matowy bałagan!
W trakcie stosowania formuł na granice ciągów warto rozważyć skorzystanie z kreatywnych rozwiązań, takich jak rysowanie wykresów! Takie podejście pomagają zobaczyć, jak zachowuje się ciąg w miarę wzrostu. Oczywiście, równie istotne pozostaje pamiętanie o definicji granicy ciągu jako pewnego limesu. Użycie definicji oraz eleganckich uproszczeń matematycznych sprawia, że obliczenia stają się znacznie bardziej przejrzyste i, co najważniejsze, poprawne.
Na koniec, jeśli uznajesz, że samodzielne obliczanie granic ciągów wydaje się zbyt trudne, nie wahaj się skorzystać z technologii! Kalkulatory online, takie jak Wolfram Alpha, stanowią prawdziwych matematycznych pomocników, którzy nie tylko obliczą granice, ale także dostarczą zrozumiałych wyjaśnień krok po kroku. Oto kilka korzyści płynących z ich używania:
- Możliwość szybkiego znalezienia granic różnych ciągów.
- Oferowanie krok po kroku rozwiązań, które pomagają zrozumieć proces obliczeń.
- Dostępność z wielu urządzeń, co umożliwia korzystanie w dowolnym miejscu i czasie.
- Rozwiązywanie bardziej skomplikowanych problemów matematycznych.
Pamiętaj – matematyka to nie tylko nieustanne zmagania, lecz także doskonała zabawa i możliwość odkrywania nowych, ciekawych metod!
| Błąd | Opis | Jak unikać |
|---|---|---|
| Niepoprawne uproszczenia | Zgubne efekty przy podejmowaniu działań arytmetycznych na granicach ciągów. | Przypomnij sobie twierdzenie o działaniach arytmetycznych na granicach. |
| Dzielenie przez rozbieżne ciągi | Może prowadzić do zgubnych skutków, zwłaszcza gdy dany ciąg dąży do nieskończoności. | Unikaj dzielenia przez takie ciągi; rozważ odwrotność w kontekście granic. |
| Brak wizualizacji | Nie używanie wykresów może utrudniać zrozumienie zachowania ciągu. | Rysuj wykresy, aby lepiej zobaczyć zmiany w miarę wzrostu. |
| Nieznajomość definicji granicy | Pominięcie definicji może prowadzić do błędów w obliczeniach. | Regularnie przypominaj sobie definicję granicy ciągu. |
| Niechęć do korzystania z technologii | Samodzielne obliczanie granic może wydawać się zbyt trudne. | Skorzystaj z kalkulatorów online, takich jak Wolfram Alpha, dla szybkich i jasnych rozwiązań. |